ΒΙΟΠΛΗΡΟΦΟΡΙΚΗ
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ
ΕΥΡΕΣΗ ΜΟΤΙΒΩΝ ΚΑΙ ΑΝΑΛΥΣΗ ΠΕΡΙΟΔΙΚΟΤΗΤΩΝ ΣΕ ΑΜΙΝΟΞΙΚΕΣ ΑΚΟΛΟΥΘΙΕΣ
Θεόδωρος Δ. Λιακόπουλος & Σταύρος Ι. Χαμόδρακας
Tομέας Βιολογίας Κυττάρου και Βιοφυσικής
Τμήμα Βιολογίας
Παν/μιο Αθηνών
Φεβρουάριος 2002


Φεβρουάριος 2002
Πολλές φορές μια άγνωστη πρωτεΐνη μοιάζει τόσο λίγο στην ακολουθία με πρωτεΐνες γνωστής δομής, ώστε να μη μπορεί να γίνει στοίχιση και έτσι η ομοιότητα να μην ανιχνεύεται. Σε κάποιες από τις περιπτώσεις αυτές, είναι εφικτό η συγγένεια να εντοπιστεί από την ύπαρξη στην ακολουθία μιας ορισμένης συστοιχίας αμινοξικών τύπων, γνωστής ως πρότυπο, μοτίβο, υπογραφή, αποτύπωμα (pattern, motif, signature, fingerprint). Η ύπαρξη των μοτίβων αυτών είναι αναμενόμενη, μια και σε ορισμένες περιοχές της πρωτεΐνης επιβάλλεται να υπάρχει εντελώς συγκεκριμένη δομή, προκειμένου να εμφανίζεται π.χ. ενζυμική δραστικότητα ή ειδικότητα πρόσδεσης. Η απαίτηση αυτή περιορίζει πάρα πολύ την εξέλιξη των περιοχών αυτών της ακολουθίας, οι οποίες είναι μικρές σε μήκος αλλά έχουν καθοριστική σημασία.
Η χρήση μοτίβων με σκοπό την εύρεση λειτουργίας από την ακολουθία (για πρωτεϊνες από μετάφραση γονιδιωμάτων
ή cDNA), έχει εξελιχθεί σε μια από τις βασικές τεχνικές της ανάλυσης ακολουθιών. Τα μοτίβα συντάσσονται με τρόπο
τέτοιο ώστε να είναι κατανοητά από υπολογιστικά εργαλεία, τα οποία έχουν τη δυνατότητα να τα αναζητούν ακόμα και σε
ολόκληρες βάσεις ακολουθών. Και τα ίδια τα μοτίβα οργανώνονται σε βάσεις δεδομένων, όπως είναι η PROSITE, που
περιέχει τόσο patterns όσο και profiles (http://www.expasy.ch/prosite/). Μια άλλη σημαντική βάση είναι η PRINTS
(http://www.bioinf.man.ac.uk/dbbrowser/PRINTS/).
Παραδείγματα:
[AC]-x-V-x(4)-{ED}.
Αυτό μεταφράζεται ως: [Ala ή Cys]-οτιδήποτε-Val- οτιδήποτε - οτιδήποτε - οτιδήποτε - οτιδήποτε -{οτιδήποτε εκτός από Glu ή Asp}.
<A-x-[ST](2)-x(0,1)-V.
Αυτό πρέπει να βρίσκεται στο αμινοτελικό άκρο, και μεταφράζεται ως: Ala- οτιδήποτε -[Ser ή Thr]-[Ser ή Thr]-(οτιδήποτε ή κανένα)-Val
Αρκετές πρωτεϊνικές οικογένειες, καθώς και δομικές ή λειτουργικές επικράτειες (domains), δε μπορούν να προσδιοριστούν ούτε με τη χρήση patterns, εξαιτίας ιδιαίτερα μεγάλης ποικιλότητας στις ακολουθίες. Ο προσδιορισμός τέτοιων οικογενειών ή επικρατειών γίνεται με τεχνικές πινάκων βαρών (weight matrices), όπως είναι τα profiles ή τα Hidden Markov Models. Σήμερα τα περισσότερα μοτίβα που προσδιορίζονται και κατατίθενται στις βάσεις δεδομένων όπως η Prosite, είναι πλέον τέτοιου τύπου.
Σε μια νέα ομάδα ακολουθιών που μοιάζουν, αλλά δεν έχει ακόμα βρεθεί κάποιο μοτίβο που να τις αναγνωρίζει ως οικογένεια, μπορούμε με τα κατάλληλα προγράμματα να παράγουμε μια σειρά από πιθανά μοτίβα. Τέτοια εργαλεία είναι π.χ.:
Μπορούμε να χρησιμοποιήσουμε το πρόγραμμα ProfileScan για να ανιχνεύσουμε ταυτόχρονα σε μια ακολουθία την ύπαρξη μοτίβων τριών διαφορετικών τύπων: Patterns, Profiles τύπου Prosite, Hidden Markov Model Profiles (ουσιαστικά, υπάρχει αντιστοιχία μεταξύ των δύο τελευταίων αν και το θεωρητικό υπόβαθρο στο οποίο αναπτύχθηκαν είναι διαφορετικό). Στη φόρμα που παρέχεται στη διεύθυνση http://hits.isb-sib.ch/cgi-bin/PFSCAN εισάγουμε την άγνωστη ακολουθία και επιλέγουμε αναζήτηση έναντι των patterns και των profiles της βάσης δεδομένων Prosite, καθώς και των profiles της βάσης δεδομένων Pfam.
Είναι χαρακηριστικό ότι δεν είναι όλα τα patterns της ίδιας σημαντικότητας. Επιπλέον, κάποια από αυτά αφορούν απλά πιθανές θέσεις μεταμεταφραστικής τροποποίησης, ενώ κάποια άλλα αφορούν περιοχές που προσδίδουν χαρακτηριστική δομή και λειτουργικότητα. Σε γενικές γραμμές τα αποτελέσματα χαρακτηρίζονται ως σημαντικά ή μη με τα σύμβολα ! και ? αντίστοιχα. Στα profiles η σημαντικότητα προσεγγίζεται με στατιστική ανάλυση, και σημαντικό θεωρείται το αποτέλεσμα που έχει ικανοποιητική τιμή E (εκφράζει την πιθανότητα η ακολουθία να ικανοποιεί το profile κατά τύχη). Στα patterns, σημαντικό θεωρείται ένα αποτέλεσμα αν αφορά pattern που δίνει γενικά λίγα εσφαλμένα θετικά αποτελέσματα (false positives, δηλαδή απαντάται σε ακολουθίες που δεν θα αναμενόταν). Σε κάθε περίπτωση, είναι απαραίτητο να παρατηρήσουμε σε ποια ή ποιες περιοχές της ακολουθίας εμφανίζεται το μοτίβο, και επιπλέον ακολουθώντας τους συνδέσμους από τη σελίδα των αποτελεσμάτων να μελετήσουμε την τεκμηρίωση (documentation) του μοτίβου. Η τεκμηρίωση περιλαμβάνει στοιχεία για τη δομική και λειτουργική σημασία του μοτίβου, τη σημαντικότητά του, καθώς και για πιθανούς κινδύνους από τη χρήση του, λόγω αβεβαιότητας. Επιπλέον, περιέχει αναφορές σε επιστημονικά άρθρα σχετικά με αυτό. Έτσι, είναι δυνατό να αποκομίσουμε σημαντικές πληροφορίες για την άγνωστη ακολουθία.
Μπορούμε να επαναλάβουμε τη διαδικασία για μια σειρά από ακολουθίες διαφορετικού τύπου (π.χ. από διάφορα ένζυμα, υποδοχείς, δομικές πρωτεϊνες) τις οποίες θα ανασύρουμε από βάσεις δεδομένων όπως η SwissProt.
Στις ακολουθίες DNA και πρωτεϊνών παρατηρούνται συχνά περιοδικά μοτίβα και διαδοχικές επαναλήψεις. Στο DNA, ο εντοπισμός τέτοιων περιοδικοτήτων μπορεί να αποκαλύψει δομικά και λειτουργικά χαρακτηριστικά του μορίου (π.χ. την ύπαρξη Z-DNA ή μεταγραφόμενων περιοχών). Στις ινώδεις (δομικές) πρωτεΐνες, η μελέτη των περιοδικοτήτων βοηθά στη διαλεύκανση της μοριακής δομής, μέσω της αρχής της στερεοδιαταξικής ισοδυναμίας, ενώ καταδεικνύει πιθανούς τρόπους συγκρότησης υπερμοριακών δομών. Χαρακτηριστικά παραδείγματα περιοδικοτήτων έχουν μελετηθεί στις ακολουθίες πρωτεϊνών όπςς η τροπομυοσίνη (McLachlan and Stewart, 1976), η μυοσίνη (McLachlan, 1993), οι κερατίνες (McLachlan,1978) και το κολλαγόνο (McLachlan, 1977).
Δύο βασικές μέθοδοι ανάλυσης έχουν χρησιμοποιηθεί για τον εντοπισμό διαδοχικών επαναλήψεων ή μοτίβων: Ανάλυση Fourier και μελέτη εσωτερικής ομολογίας. Πρόσφατα αναπτύχθηκαν κι άλλες μεθοδολογίες, βασισμένες σε μετασχηματισμούς κατά Fourier (McLachlan, 1993; Cheever et al., 1991; Cornette et al., 1987; Viari et al., 1990; Lazovic, 1 996; Veljkovic et al., 1985), ή μαθηματικές θεωρίες όπως η αμοιβαία πληροφορία (Korotkov et al., 1997) και τα φράκταλς (Voss, 1992).
Θα αναλύσουμε με το πρόγραμμα FT (http://biophysics.biol.uoa.gr/FT/) την ακολουθία της πρωτεϊνικής ακολουθίας CCC4. Είναι μια πρωτεΐνη του χορίου της μύγας Ceratitis capitata. Χαρακτηριστικό της γνώρισμα είναι η έντονη επανάληψη του pattern 'SYSAPAP'. Η Fasta γραφή της ακολουθίας είναι η εξής:
>CCC4 MNRFLCTFAAIVAVANGYAVGGGGGYGGRGGSGTVIGGQAYQILPALQVQTIAAAGGSSAGYGGSSAGYGASSGSYGASS GGYGGSSNGYGASSAPSIDIGQLLAAVGGDLTAQEAAQLVNSLPSAGGPIIDTSGSSAGSSHQGSYPSGGNLAYVIQSGG SSYSAPAPAASYSAPAPAPAASYSAPAPSYSAPAPAPAPSYSAPAPSYSAPAPSYSAPAPAPAPAAYSAPAPAVYSAPAP AAYSAPAPAVYSAPAPAPAPAAYSAPAPAAYSAPAPAAYSAPASSGYGASAPAAAAPAAAHQPSAAAARSYISGSYGAAY APAPAPAAGGAY
Την ακολουθία μπορούμε να τη βρούμε και στη σελίδα http://biophysics.biol.uoa.gr/FT/sample1.html
Στη φόρμα εισόδου των δεδομένων, την οποία βλέπουμε επιλέγοντας 'Execute the program', τοποθετούμε την ακολουθία, και στην περιοχή 'format' επιλέγουμε 'FASTA'.
Πατώντας στο πλήκτρο Check, βλέπουμε τις εξής πληροφορίες:
i. το μήκος της ακολουθίας (332) (επάνω από την περιοχή κειμένου που περιέχει την ακολουθία),
ii. το μικρότερο "μέγεθος εμβάπτισης" (embedding size) που μπορεί να χρησιμοποιηθεί από το πρόγραμμα (512) (κάτω από την περιοχή κειμένου),
iii.το πλήθος εμφάνισης του κάθε αμινοξικού τύπου στην ακολουθία (εμφανίζεται στην περιοχή 'Statistics').
Βλέπουμε έτσι πως η Αλανίνη είναι το πιο συχνά απαντώμενο κατάλοιπο (96), ενώ ακολουθεί η Σερίνη (54), η Γλυκίνη (46) και η Προλίνη (45). Αν υπολογίσουμε τα ποσοστά, έχουμε αντίστοιχα 28.9% Αλανίνη, 16,2% Σερίνη, 13.8% Γλυκίνη και 13.5% Προλίνη.
Αποφασίζουμε να μετρήσουμε την περιοδικότητα του πιο συχνού αμινοξέος, της Αλανίνης, οπότε επιλέγουμε βάρος 1 για την Αλανίνη στην περιοχή Selection of residues , θέτουμε το όριο (cutoff) στο 0 για να πάρουμε μία συνεχή γραφική παράσταση και επιλέγουμε εύρος περιοδικοτήτων μεταξύ 2 (ελάχιστη, min period) και 50 (μέγιστη, max period).
Πατώντας 'Submit', πέρνουμε τη σελίδα με τα αποτελέσματα, η οποία αποτελείται από τρία μέρη: σύνοψη των δεδομένων που δώσαμε, πίνακας με τα αποτελέσματα και γραφική παράσταση (εφόσον επιλέξαμε 'HTML page' στη φόρμα εισόδου) η οποία απεικονίζει το συσχετισμό μεταξύ περιοδικότητας και έντασης.
Σ'αυτή την παράσταση, βλέπουμε πως οι υψηλότερες εντάσεις παρατηρούνται μεταξύ περιοδικοτήτων 2 και 7 καταλοίπων.
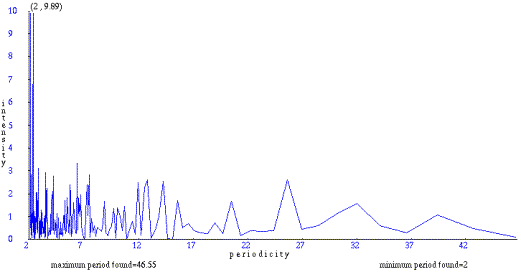
(Σημείωση: Θα μπορούσαμε να είχαμε πάρει μια πιο ομαλή γραφική παράσταση, επιλέγοντας μεγαλύτερο "μέγεθος εμβάπτισης"-embedding size.)
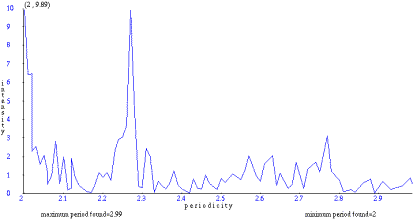
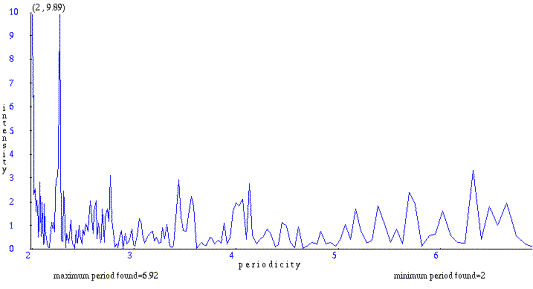
Για να δούμε περισσότερες λεπτομέρειες, επιστρέφουμε στη φόρμα εισόδου πατώντας το πλήκτρο Back του browser, και θέτουμε μέγιστη περιοδικότητα 7. Τώρα, διακρίνουμε στη νέα γραφική παράσταση ότι οι υψηλότερες εντάσεις αντιστοιχούν σε περιοδικότητες κάτω του 3.
Ξανά επιλέγουμε μικρότερο εύρος περιοδικοτήτων στη φόρμα εισόδου. Βλέπουμε το αποτέλεσμα για εύρος μεταξύ 2 και 3:
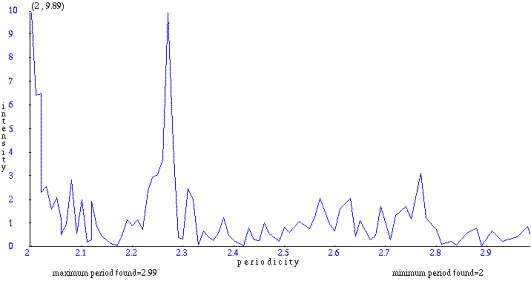
Μπορούμε να αποκλείσουμε τις χαμηλές εντάσεις, θέτοντας ένα όριο μεγαλύτερο από 0 (cutoff, αναφέρεται στην ελάχιστη τιμή έντασης που απεικονείζεται στο γράφημα). Έτσι θα δούμε σε ιστόγραμμα τις περιοδικότητες που είναι μεγαλύτερες ή ίσες με το όριο. Για όριο 2.5, η γραφική μας παράσταση γίνεται:
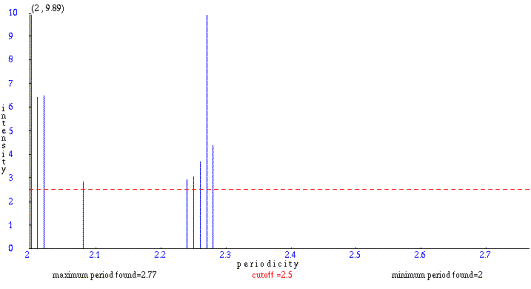
Μπορούμε να εξετάσουμε και μόνο ένα κομμάτι της ακολουθίας μας, αλλάζοντας τις προεπιλεγμένες τιμές Start residue και End residue (αρχικό και τελικό κατάλοιπο). Μεταξύ των θέσεων 162 και 278, το pattern 'SYSAPAP' επαναλαμβάνεται 13 φορές, με την παρεμβολή 0 ως 5 καταλοίπων ανάμεσα σε κάθε επανάληψη. Μπορούμε, άρα, να αναμένουμε περιοδικότητα που τείνει στο 9. Στην πράξη, το πρόγραμμα για τα κατάλοιπα S, Y και P μας δίνει περιοδικότητα 8.98. Οι εντάσεις μεταξύ 7.12 και 7.82 που υπολογίζονται για την περιοδικότητα αυτή, για τα συγκεκριμένα κατάλοιπα, μας πληροφορούν πως η πιθανότητα το αποτέλεσμα να οφείλεται στην τύχη είναι πάρα πολύ μικρή (McLachlan, 1977). Ακολουθεί η γραφική παράσταση για τις περιοδικότητες της Προλίνης (P) μεταξύ 3 και 50, για την περιοχή [162, 278].
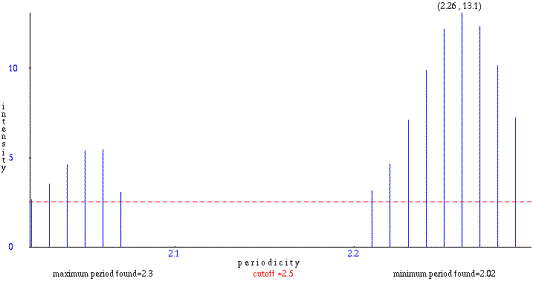
Τα κατάλοιπα που απαντούν μεταξύ διαδοχικών εμφανίσεων του pattern 'SYSAPAP' είναι μόνο τα 'A' και 'P'. Άρα, στο συγκεκριμένο κομμάτι της ακολουθίας υπάρχει στην πραγματικότητα επανάληψη ενός μοτίβου 'S Y S (A|P)+', δηλαδή η συστοιχία 'S', 'Y' και 'S' ακολουθούμενη από επαναλήψεις των 'A' ή 'P'. Μπορούμε να καταδείξουμε την περιοδικότητα (8.98) για αυτές τις δύο ομάδες καταλοίπων, επιλέγοντας 'S' και 'Y', και μετά 'A' και 'P'. Αντίστοιχα, οι εντάσεις που παίρνουμε είναι 17.05 και 16.50. Για να επαληθεύσουμε ότι οι ομάδες αυτές εναλάσσονται μεταξύ τους, δίνουμε στην καθεμία διαφορετικό βάρος (weight). Δίνοντας, για παράδειγμα, βάρη 1 και –1 στις δύο ομάδες, η περιοδικότητα 8.98 εμφανίζεται με ένταση 17.10.
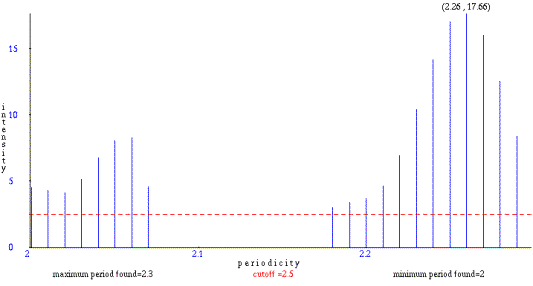
Αναλύοντας το καθένα ξεχωριστά, τα κατάλοιπα S, Y και P έχουν υψηλές εντάσεις στην περιοδικότητα 8.98 (αντίστοιχα 7.63, 7.12 και 7.82), ενώ για την Α δεν υπάρχει σημαντική ένταση. Όταν όμως επιλέγουμε όλα τα κατάλοιπα του μοτίβου μαζί, αναθέτοντας βάρος 1 στο καθένα, δεν είναι δυνατό να απομονώσουμε την ένταση. Για το λόγο αυτό, πρέπει τελικά να αναθέσουμε διαφορετικό βάρος σε κάθε τύπο καταλοίπου, και να ορίσουμε έτσι το μοτίβο. Ορίζοντας, για παράδειγμα, βάρος 1 για την Α, 2 για την P, 3 για την S και 4 για την Y, οδηγούμαστε σε πολύ υψηλή ένταση (9.77) για την περιοδικότητα 8.98.
Aggeli,A, Hamodrakas,S.J., Komitopoulou,K. and Konsolaki,M.(1991) Tandemly repeating peptide motifs and their secondary structure in Ceratitis capitata eggshell proteins Ccs36 and Ccs38. Int. J. Biol. Macromol., 13, 307–315.
Cheever,E.A., Overton,G.C. and Searls,B.B. (1991) Fast fourier transform-based correlations of DNA sequences using complex plane encoding. Comput. Applic. Biosci., 7, 143–154.
Cornette,J.L., Cease,K.B., Margalit,H., Spouge,J.L., Berzofsky,J.A. and DeLisi,C. (1987) Hydrophobicity scales and computational techniques for detecting amphipathic structures in proteins. J. Mol. Biol., 195, 659–685.
Hamodrakas,S.J., Ekmetzoglou,T. and Kafatos,F.C. (1985) Amino acid periodicities and their structural implications for the evolutionarily conservative central domain of some silkmoth chorion proteins. J. Mol. Biol., 186, 583–589.
Korotkov,E.V., Korotkova,M.A. and Tulko,J.S. (1997) Latent sequence periodicity of some oncogenes and DNA-binding protein genes. Comput. Applic. Biosci., 13(1), 37–44.
Lazovic,J. (1996) Selection of amino acid parameters for Fourier transform-based analysis of proteins. Comput. Applic. Biosci., 12(6), 553–562.
McLachlan,A.D. (1977) Analysis of periodic patterns in amino acid sequences: collagen. Biopolymers, 16, 1271–1297.
McLachlan,A.D. (1978) Coiled coil formation and sequence regularities in the helical regions of a-keratin. J. Mol. Biol., 124, 297–304.
McLachlan,A.D. (1993) Multichannel fourier analysis of patterns in protein sequences. J. Phys. Chem., 97, 3000–3006.
McLachlan,A.D. and Stewart,M. (1976) The 14-fold periodicity in a-tropomyosin and the interaction with actin. J. Mol. Biol., 103, 271–298.
Veljkovic,V., Cosic,I. and Dimitrijevic,B. (1985) Is it possible to analyze DNA and protein sequences by the methods of digital signal processing? IEEE Trans. Biomed. Eng., 32(5), 337–341.
Viari,A., Soldano,H. and Ollivier,E. (1990) A scale-independent signal processing method for sequence analysis. Comput. Appl. Biosci., 6, 71–80.
Vlahou,D., Konsolaki,M., Tolias,P., Kafatos,F.C. and Komitopoulou, M. (1997) The autosomal chorion locus of the medfly Ceratitis capitata. I. Conserved synteny, amplification and tissue specificity but sequence divergence and altered temporal regulation. Genetics, 147(4), 1829–1842.
Voss,R.F. (1992) Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett., 68, 3805–3808.