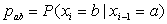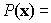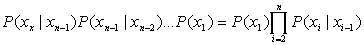ΕΙΣΑΓΩΓΗ

Τα τελευταία χρόνια, η ανάγκη για την επίλυση όλο και πιο συνθετων βιολογικών προβλημάτων, έχει οδηγήσει στην εφαρμογή σε βιολογικά προβλήματα, πολύπλοκων μαθηματικών και υπολογιστικών μοντέλων. Τα πιο γνωστά και πιο χρησιμοποιημένα από τα μοντέλα αυτά είναι τα Hidden Markov Models (HMM) και τα Tεχνητά Νευρωνικά Δίκτυα (Artificial Neural Networks). Παρόμοια μοντέλα χρησιμοποιήθηκαν και χρησιμοποιούνται και σε άλλα ερευνητικά πεδία όπως η επεξεργασία εικόνας, ήχου και σήματος στην ηλεκτρονική και στις τηλεπικοινωνίες, και γένικά χρησιμοποιούνται ευρέως σαν pattern recognition methods.

Απο τη μια μεριά η εμφάνιση όλο και πιο πολύπλοκων βιολογικών προβλημάτων και ερωτημάτων που τίθενται λόγω της ραγδαίας αύξησης των δεδομένων που συσσωρεύονται χρόνο με το χρόνο (ακολουθίες DNA και πρωτεϊνών που κατατίθενται στις βάσεις δεδομένων) και από την άλλη η διαρκής εξέλιξης της τεχνολογίας των Η/Υ, χάρη στην οποία έχει γίνει εφικτή η πρόσβαση από όλους σε μηχανήματα υψηλής υπολογιστικής ισχυος, έχουν οδηγήσει την τελευταία δεκαετία ιδίως, σε ευρεία χρησιμοποίηση τέτοιων μοντέλων στη βιολογία (βιοπληροφορική). Από τα μοντέλα αυτά, τα Hidden Markov Models (HMM) είναι κατα βάση στοχαστικά, με ξεκάθαρη δηλαδη πιθανοθεωρητική ερμηνεία, ενώ τα Tεχνητά Νευρωνικά Δίκτυα (Artificial Neural Networks), είναι περισσότερο προσεγγιστικές τεχνικές τεχνητής νοημοσύνης (artificial intelligence), και τα δυο όμως είναι ιδιαίτερα χρήσιμα στην αποκάλυψη των πολύπλοκων και μη γραμμικών σχέσεων που εμφανίζονται μεταξύ πρωτοταγούς δομής των μακρομορίων και της τρισδιαστατης δομής και λειτουργίας τους.

Μέθοδοι οι οποίοι χρησιμοποιούν Αλυσίδες Markov (Markov Chains), έχουν προταθεί εδώ και περίπου μια δεκαετία για την αναγνώριση γονιδίων σε ολόκληρα γονιδιώματα (Borodovsky and McIninch, 1993). Τα Hidden Markov Models (HMM) έχουν προταθεί για αναγνώριση δευτεροταγούς δομής αλλα και σαν μέθοδος κατασκευής profiles (Eddy, 1996). Πρόσφατα τα ΗΜΜ, έχουν φανεί ιδιαίτερα ισχυρά, λογω της περίπλοκης αρχιτεκτονικής τους, στον εντοπισμό διαμεμβρανικών τμημάτων σε πρωτεϊνες, με χαρακτηριστικά παραδείγματα το TMHMM (Krogh, et al. 2001) και το HMMTOP (Tusnady and Simon, 1998; Tusnady and Simon, 2001).

Αντίστοιχα εργαλεία που βασίζονται σε κάποιο Νευρωνικό Δίκτυο, έχουν προταθεί επίσης για τον εντοπισμό διαμεμβρανικών περιοχών (Fariselli and Casadio,1998; Pasquier and Hamodrakas,1999) για την πρόγνωση διαμεμβρανικών β-πτυχωτων επιφανειών (Diederichs et all, 1998), αλλά και για την πρόγνωση του τύπου μιας άγνωστης πρωτεϊνης (Pasquier et al, 2001)

Α) Αλυσίδες Markov (Markov Chains) και Hidden Markov Model (HMM)

Οι Αλυσίδες Markov (Markov Chains), είναι πιθανοθεωρητικά (στοχαστικά) μοντέλα, με τα οποία περιγράφουμε και αναλύουμε τις ακολουθίες βιολογικών πολυμερών όπως το DNA και οι πρωτεϊνες. Πρέπει εδώ να τονιστεί ότι το μοντέλο Markov θεωρείται από πολλούς ερευνητές ως το πιο φυσικό για να περιγράψει αλληλουχίες μεγαλομορίων όπως του DNA αλλά και των Πρωτεϊνών, και αυτό φαίνεται διαισθητικά φυσικό καθώς αυτή η εξάρτηση φαίνεται να προσεγγίζει την έννοια της πληροφορίας που εμπεριέχεται σε μια αλληλουχία. Ήδη από την δεκαετία του 70 τα μοντέλα αυτά χρησιμοποιούνταν και χρησιμοποιούνται με σκοπό την αναγνώριση και επεξεργασία εικόνας, ήχου κ.α. και υπάρχει πλούσια βιβλιογραφία πάνω στα θέματα αυτά. Η πιο απλή εξήγηση για τα παραπάνω είναι το γεγονός ότι σε οποιοδήποτε κωδικοποιημένο σύστημα επικοινωνίας, όπως στις φυσικές γλώσσες, υπάρχει μια εσωτερική δομή πoυ καθορίζει κάποιο είδος εξάρτησης των συμβόλων. Για παράδειγμα, στην αγγλική γλώσσα το γράμμα Q ακολουθείται σχεδόν πάντοτε από το U, άρα η πιθανότητα να εμφανιστεί το U σε μια θέση δεν είναι πάντα ίδια αλλά εξαρτάται από το αν προηγήθηκε το Q. Για την ακρίβεια ο ίδιος ο Ρώσος Μαθηματικός Andrey Markov (1856-1922) οδηγήθηκε στην σύλληψη της έννοιας των ομώνυμων αλυσίδων μελετώντας τις εναλλαγές φωνηέντων και συμφώνων σε κάποιο ποίημα του Pushkin. Έστω ότι έχουμε μια αλυσίδα π.χ. DNA

ATTGTAATCTCACGGTGTACGCGCATGCACAGTCAGT

ή μια αμινοξική αλληλουχία

AEDGPRGSDADKLIAVCLIGFVLIFVSLVCVTYTRED

Αν θεωρήσουμε ότι τα σύμβολα (νουκλεοτίδια ή αμινοξέα) δεν είναι ανεξάρτητα μεταξύ τους, αλλά το ποιο θα ακολουθήσει εξαρτάται μόνο απο το αμέσως προηγούμενο του, τότε η πιθανότητα να εμφανιστεί π.χ. καποιο b, δεδομένου ότι το αμέσως προηγούμενο του είναι α, (πιθανότητα μεταβάσεως - transition probability) θα είναι:

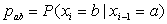
και η συνολική πιθανότητα να παρατηρηθεί η δεδομένη αλληλουχία θα είναι:

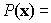
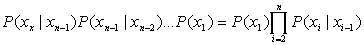
Το μοντέλο αυτό με επεκτάσεις του σε εξάρτηση, πέραν της πρώτης ταξης χρησιμοποιείται ευρέως στην ανίχνευση γονιδίων σε νεο-ανακαλυφθείσες ακολουθίες DNA (Borodovsky and McIninch, 1993).

Μια επέκταση των αλυσίδων Markov, είναι και το Hidden Markov Model (HMM). Στο μοντέλο αυτό, έχουμε μια ακολουθία συμβόλων και μια αλληλουχία καταστασεων π.χ.

..AEDGPRGSDADKLIAVILIGFVLIFVALVCVTYTRED..

..------------++++++++++++++++++-------..

Στη συγκεκριμμένη περίπτωση με (+) συμβολίζουμε τα διαμεμβρανικά τμήματα της ακολουθίας, ενώ με (-) τα μη διαμεμβρανικά. Η βασική διαφορά απο το προηγούμενο μοντέλο είναι ότι τώρα αλυσίδα Markov, συνιστούν όχι τα ίδια τα σύμβολα (αμινοξέα) αλλά η αλληλουχία των καταστασεων (+,-). Ετσι έχουμε τώρα τις πιθανότητες μεταβάσεως

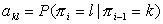
και σε κάθε κατασταση (state) ισχύουν διαφορετικές πιθανοτητες εμφάνισης των συμβόλων (αμινοξέα). Οι πιθανότητες αυτές ονομάζονται πιθανότητες γενέσεως (emission probabilities) και όπως είναι φυσικό είναι δεσμευμένες στην κατασταση που βρισκόμαστε (άλλα αμινοξέα έχουν προτιμηση για τα διαμεμβρανικά τμήματα και άλλα για τα μη διαμεμβρανικά).

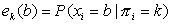
Στο παρακάτω διάγραμμα φαίνεται σχηματικά το ΗΜΜ που περιγράψαμε παραπάνω.

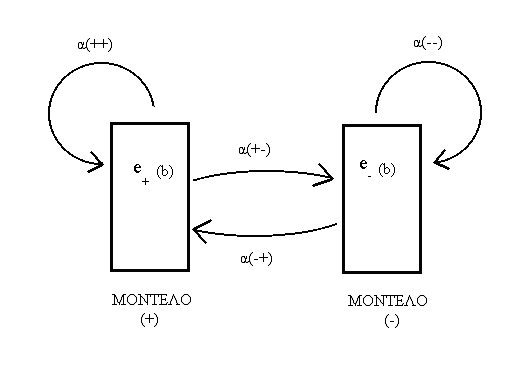
Η πολύ απλή ερμηνεία που έχει το ΗΜΜ στην περίπτωση των διαμεμβρανικών τμημάτων μιας πρωτεϊνης, είναι η εξής: είναι γνωστό ότι τα διαμεμβρανικά τμηματα απαρτίζονται κυρίως απο υδρόφοβα αμινοξέα, άρα η πιθανότητα να εμφανιστεί π.χ. Ισολευκίνη είναι μεγαλύτερη σε ένα διαμεμβρανικό τμήμα είναι μεγαλύτερη απο ότι σε ένα μη διαμεμβρανικό. Επίσης τα αμινοξέα στα διαμεμβρανικά τμήματα διαδέχονται το ένα το άλλο, και έτσι είναι πιο πιθανό όταν έχει προηγηθεί ενα αμινοξύ που ανήκει σε τέτοιο τμήμα, το επόμενο του να είναι επίσης μέρος της διαμεμβρανικής περιοχής.

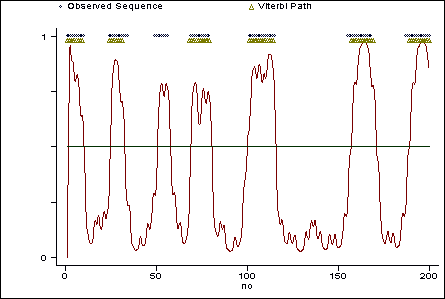
Ενα ΗΜΜ, αφού υπολογιστούν οι παραμέτροι του (πιθανότητες μεταβάσεως κλπ) απο ένα σύνολο πρωτεϊνών γνωστής δομής (training set), χρησιμοποιείται για την πρόγνωση-αποκωδικοποίηση, σε ένα σύνολο πρωτεϊνών άγνωστης δομής (test set). Οι μέθοδοι αποκωδικοποίησης, δηλαδή εύρεσης της αλληλουχίας των καταστάσεων εάν είναι γνωστή αλληλουχία των συμβόλων, είναι βασικά 2, η αποκωδικοποίηση Viterbi, και η εκ των υστέρων αποκωδικοποίηση (posterior decoding). Συνήθως σε περιπτώσεις πολύπλοκων μοντέλων , είναι πιο χρήσιμη η εκ των υστέρων αποκωδικοποίηση.

Στο διαδίκτυο υπάρχουν προγράμματα τα οποια χρησιμοποιούν ΗΜΜ για την πρόβλεψη διαμεμβρανικών τμημάτων πρωτεϊνών απο την ακολουθία τους

Β) Tεχνητά Νευρωνικά Δίκτυα (Artificial Neural Networks)

Μια άλλη σύγχρονη υπολογιστική μέθοδος που χρησιμοποιείται στη μελέτη των ακολουθιών των μακρομορίων, είναι τα Tεχνητά Νευρωνικά Δίκτυα (Artificial Neural Networks). Η μέθοδος αυτή έχει χρησιμοποιηθεί επίσης για αναγνώριση και επεξεργασία εικόνας, ήχου και γενικά για pattern recognition. Με τη μέθοδο αυτή ο Η/Υ, προσπαθεί να προσομοιώσει τον τρόπο με τον οποίο «μαθαίνει» ο ανθρώπινος εγκέφαλος μέσω των νευρώνων.

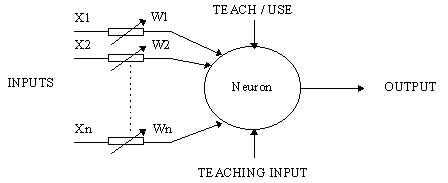
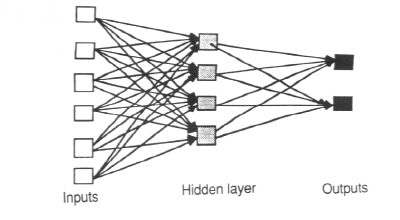
Στην πράξη ένα Νευρωνικό Δίκτυο, πραγματοποιεί μια μη-γραμμική παλινδρόμηση (non linear regression). Ας υποθέσουμε ότι έχουμε ένα set δεδομένων, στο οποίο περιλαμβάνονται μετρήσεις οποιουδήποτε τύπου. Οι μεταβλητές που έχουμε χωρίζονται σε ανέξαρτητες μεταβλητές (independent variables- predictors) οι οποίες είναι ποσότητες που μπορούμε να μετρήσουμε και βάση των οποίων θα γίνει η πρόβλεψη, καθώς επίσης και σε εξαρτημένες μεταβλητές (dependent variables- outputs) τις οποίες πρέπει να προβλέψουμε. Με την κλασσική στατιστική (Linear Regression, Logistic Regression, ANOVA, MANOVA κλπ) είμαστε σε θέση να ανιχνεύσουμε τις γραμμικές συνεισφορές των ανεξαρτήτων μεταβλητών, στις εξαρτημένες. Το Νευρωνικό Δίκτυο παρεμβάλλει μεταξύ των ανεξαρτήτων μεταβλητών (inputs) και των εξαρτημένων (outputs), μιας σειράς απο κρυφές μεταβλητές-νευρώνες (hidden units) και επιτρέπει σε καθε input να μπορεί να συνδεεται, να συνισφέρει δηλαδή σε καθε hidden unit, και αυτά μετη σειρά τους συνισφέρουν στο output. Η συνεισφορα κάθε νευρώνα εκφράζεται με ένα συναπτικό βάρος (weight). Το αποτέλεσμα μετα απο μια πολύπλοκη συνδεσμολογία, είναι ότι το Νευρωνικό Δίκτυο μπορεί να προσομοιώσει κάθε είδους μη-γραμμική σχεση μεταξύ εξαρτημένων και ανεξάρτητων μεταβλητων. Παρακάτω φαίνεται η συνδεσμολογία ενος ΝΔ, με 6 inputs, 4 κρυφές μονάδες (hidden units), και 2 outputs.

Παρακάτω φαίνεται ενα δείγμα αρχείου όπου έχουμε αποθηκευμένες 4 ανέξαρτητες μεταβλητές (SepLen, SepWid, PetLen, PetWid) και 3 ψευδομεταβλητές outputs (dummy variables) που αντιστοιχουν στο είδος του φυτού (Species1, Species2, Species3). Η μεταβλητή Flower, συμβολίζει τον α/α των λουλουδιών ενώ η Zrandom είναι τυχαίος θόρυβος.

Flower 	SepLen 	       SepWid  	PetLen  PetWid      	ZRandom     Species1 Species2 Species3
1	5.9		3	5.1	1.8		0.5799		1	0	0
2	6.2		3.4	5.4	2.3		0.5863		1	0	0
3	6.5		3	5.2	2		0.39		1	0	0
4	6.3		2.5	5	1.9		-0.2844		1	0	0
5	6.7		3	5.2	2.3		0.4847		1	0	0
6	6.7		3.3	5.7	2.5		-1.3032		1	0	0
7	6.8		3.2	5.9	2.3		-1.1097		1	0	0
8	5.8		2.7	5.1	1.9		-1.2641		1	0	0
.	.		.	.	.		.		.	.	.	
50	6.3		3.3	6	2.5		-0.8097		1	0	0
51	5.1		2.5	3	1.1		-0.5423		0	1	0
52	6.2		2.9	4.3	1.3		-0.9649		0	1	0
53	5.7		2.9	4.2	1.3		-0.34		0	1	0
54	5.7		3	4.2	1.2		0.1504		0	1	0
.	.		.	.	.		.		.	.	.	
104	4.8		3	1.4	0.3		-0.1982		0	0	1
105	5.1		3.8	1.9	0.4		0.9745		0	0	1
106	5		3.5	1.6	0.6		1.3348		0	0	1
107	4.4		3.2	1.3	0.2		-0.9846		0	0	1
108	4.5		2.3	1.3	0.3		0.2328		0	0	1
.	.		.	.	.		.		.	.	.	

Ενα ΝΔ πριν χρησιμοποιηθεί σε άγνωστα δεδομένα (test), πρέπει να εκπαιδευθεί (train) σε δεδομένα για τα οποία γνωρίζουμε το output, πρέπει να βρεθεί δηλαδή το σετ των βαρών (weights) και η συνδεσμολογία η οποία βελτιστοποιεί την διακριτική ικανότητα της μεθοδου. Συνήθως σε δεδομένα βιολογικού τύπου χρησιμοποιείται ο αλγοριθμος Back Propagation. Για την εφαρμογή των ΝΔ, σε ανάλυση π.χ. πρωτεϊνικών ακολουθιών, πρέπει έχουμε μετρησιμα μεγέθη που αντανακλούν μια βιολογική έννοια. Έτσι π.χ. το PRED-CLASS (Pasquier et al, 2001), χρησιμοποιεί σαν inputs χαρακτηριστικά όπως η συχνότητα των διαφόρων αμινοξέων και οι περιοδικότητες τους, ενώ σαν output δίνει τον τύπο της πρωτεϊνης (ινώδης, σφαιρικη υδατοδιαλυτή, διαμεμβρανική κλπ). Τα ΝΔ μπορούν να χρησιμοποιηθούν και για πρόγνωση ιδιαίτερων χαρακτηριστικών των μεμονομένων αμινοξέων (π.χ. δευτεροταγής δομή) με τη διαφορά ότι πρέπει σαν inputs να χρησιμοποιηθούν αποτελέσματα προγενέστερης ανάλυσης (π.χ. πιθανότητες εμφάνισης του κάθε αμινοξέως στην α-έλικα, κλπ). Το PRED-TMR2 (Pasquier and Hamodrakas,1999), χρησιμοποιεί ένα τέτοιο ΝΔ, για να κάνει πρόβλεψη των διαμεμβρανικών τμημάτων μιας πρωτεϊνης.

ΠΡΑΚΤΙΚΟ ΜΕΡΟΣ

Στο πρακτικό μέρος αυτής της άσκησης, θα δούμε κάποιες πρακτικές εφαρμογές των ΗΜΜ και των ΝΔ, σε πραγματικά βιολογικά δεδομένα. Θα χρησιμοποιήσετε το αρχείο UNKNOWN_SEQUENCES.TXT, το οποίο περιέχει σε FASTA format, τις ακολουθίες 5 πρωτεϊνών. Για κάθε μια από αυτές, (χρησιμοποιήστε copy-paste) θα πρέπει να διευκρινήσετε τον τύπο της, και (αν υπάρχουν) τα διαμεμβρανικά της τμήματα.

ΒΙΒΛΙΟΓΡΑΦΙΑ

• Altschul, S. F., Madden, T. L., Schaffer, A. A., Zhang, J., Zhang, Z., Miller, W. and Lipman, D. J. (1997). Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Research 25:3389-3402.
• Borodovsky, M. and McIninch, J. (1993). GENMARK: parallel gene recognition for both DNA strands. Computers and Chemistry 17:123-133.
• Diederichs, K., Freigang, J., Umhau. S., Zeth, K. and Breed, J. (1998) Prediction by a neural network of outer membrane bstrand protein topology. Protein Science. 7:2413-2420
• Eddy, S. R. (1996). Hidden Markov models. Current Opinion in Structural Biology 6:361-365.
• Fariselli, P. and Casadio, R. (1998) HTP: a neural-network based method for predicting the topology of helical transmembrane domains in proteins. Comput. Applic. Biosci. 12(1):41-48
• Jacoboni, I., Martelli, P. L., Fariselli, P., de Pinto V. and Casadio, R. (2001) Prediction of transmembrane regions of β-barrel membrane proteins with a neural network-based predictor. Prot. Sci. 10:779-787
• Krogh, A., Larsson, B., von Heijne, G. and Sonnhammer, E. L. L. (2001) Predicting transmembrane protein topology with a Hidden Markov Model: Application to complete genomes. J. Mol. Biol. 305:567-580
• Pasquier, C. and Hamodrakas, S.J. (1999) An hierarchical artificial neural network system for the classification of transmembrane proteins. Prot. Eng., 12(8): 631-4.
• Pasquier, C., Promponas, V. I. and Hamodrakas, S. J. (2001) PRED-CLASS: Cascading neural networks for generalized protein classification and genome-wide applications. Proteins, 44:361-369.
• Tusnady, G. E. and Simon, I. (1998) Principles governing amino acid composition of integral membrane proteins: Application to topology prediction. J. Mol. Biol. 283:489-506
• Tusnady, G. E. and Simon, I. (2001) Topology of membrane proteins. J. Chem. Inf. Comput. Sci. 41:364-368